(A la parte 4 – A la parte 6)
Los ordinales
Para mejor comprensión, dividamos el contenido de esta entrada en varios ítemes:
1) “La” idea: En su primera definición, en 1883, Cantor entiende a los ordinales como una extensión del sistema de los números naturales. Los ordinales son números que "permiten seguir contando más allá del infinito". Según esta idea, el primer ordinal es el 0 y a partir de allí Cantor establece dos reglas (1) para la formación de los ordinales siguientes:
Regla 1: Dado un ordinal $\alpha $, existe siempre el ordinal siguiente, $\alpha +1$.
Regla 2: Dada cualquier secuencia creciente de ordinales, siempre hay un nuevo ordinal que es el primero que cumple que es mayor que todos ellos (2).
El primer ordinal es, como dijimos, el 0; por aplicaciones sucesivas de la primera regla obtenemos: 1, 2, 3, 4, 5,... Después de todos los números naturales la segunda regla nos dice que hay un nuevo ordinal, que Cantor llama $\omega $ (omega minúscula, u “omeguita”), luego viene $\omega +1$, $\omega +2$, $\omega +3$,... Después de todos los $\omega +n$ la segunda regla nos dice que viene otro, que es $\omega +\omega $. Luego viene $\omega +\omega +1$, $\omega +\omega +2$ y así sucesivamente. Luego de todos los $\omega +\omega +n$ viene el $\omega +\omega +\omega $, y así sucesivamente. Mucho más allá está $\omega +\omega +\omega +\omega +\dots $ infinitas veces $\omega $ y, claro está, también $\omega +\omega +\omega +\omega +\dots +1$ (donde $\omega $ aparece infinitas veces).
En resumen, los ordinales nos permiten contar así:
(Lo que sigue debe se leído en voz alta y cuando aparezcan puntos suspensivos el lector debe seguir contando muy rápidamente hasta quedarse sin aliento.)
0, 1, 2, 3, 4, 5,... (aquí infinitos números) $\omega $, $\omega +1$, $\omega +2$, $\omega +3$, $\omega +4$, $\omega +5$,... (aquí infinitos números) $\omega +\omega $, $\omega +\omega +1$, $\omega +\omega +2$, $\omega +\omega +3$, $\omega +\omega +4$, $\omega +\omega +5$,... (aquí infinitos números),... (aquí infinitas infinidades de números) $\omega +\omega +\omega +\omega +\dots \omega +\omega +\omega +\omega +\dots $, $\omega +\omega +\omega +\omega +\dots \omega +\omega +\omega +\omega +\dots + 1$, $\omega +\omega +\omega +\omega +\dots \omega +\omega +\omega +\omega +\dots + 2$ etc.
Conviene siempre tener presente esta idea: los ordinales son números que "permiten contar más allá del infinito". Ésta fue la primera idea de Cantor y la verdadera idea. En los ítemes siguientes de esta entrada desarrollaremos la definición, más formal, que dio Cantor en 1897. Más adelante daremos también la definición que dio von Neumann en 1923, pero todas ellas no son más que formalizaciones de esta idea inicial.
2) Repaso: Recordemos que un conjunto es bien ordenado si todo subconjunto no vacío de él tiene mínimo. Si (A, $\leq $) es bien ordenado diremos que $\leq $ es un buen orden para A.
3) Equivalencia: Dos conjuntos bien ordenados (A, $\leq $) y (B, $\leq $) son equivalentes si existe una función biyectiva $f : A\rightarrow B$ tal que si $x\leq y$ entonces $f(x)\leq f(y)$. En palabras simples, (A, $\leq $) y (B, $\leq $) son equivalentes si el orden en B es una “copia textual” del orden en A (véanse ejemplos en el ítem siguiente).
4) Ejemplos: vimos en la entrada anterior que en N es posible definir muchos buenos órdenes diferentes. Para describir cada orden escribiremos el ordenamiento de los números:
a) El orden usual: 0, 1, 2, 3, 4, 5,...
b) El orden en el que arbitrariamente decidimos que el 0 es mayor que todos los demás números: 1, 2, 3, 4, 5,..., 0
c) El orden en el que los impares preceden a todos los pares: 1, 3, 5, 7,..., 0, 2, 4, 6,...
d) El orden en el que intercambiamos cada impar y su siguiente: 2, 1, 4, 3, 6, 5, 8, 7,...
Tenemos que a y b no son equivalentes entre sí, pues es claro que no tienen la misma “forma”. Tampoco son equivalente a y c ni tampoco b y c. En cambio sí son equivalentes a y d, en los dos hay un primer elemento, luego otro, luego otro y así sucesivamente (En b al “y así sucesivamente” le sigue un último elemento, mientras que en c le sigue toda una nueva serie de elementos.)
5) Otros ejemplos: podemos generar otra fuente de ejemplos timando dos copias de N = {0, 1, 2, 3,...}. Para distinguir las copias, a la segunda la llamaremos N’ = {0’, 1’, 2’, 3’,...}.
El ordenamiento en N será el usual, el ordenamiento en N’ también será el usual. Convendremos además que en que cada número de N’ será mayor que cualquier número de N. Así por ejemplo 230’ es mayor que 2’, que es mayor que 999, que es mayor que 0.
a) Si tomamos sólo el 0 de N y todos los números de N’, su ordenamiento es: 0, 0’, 1’, 2’, 3’...
b) Tomemos a N le agregamos el 0’, su ordenamiento es: 0, 1, 2, 3, 4,..., 0’.
c) Tomemos tomamos todo N y N’, su ordenamiento es: 0, 1, 2, 3, 4,..., 0’, 1’, 2’, 3’,...
Los ejemplos a, b, y c del punto 4 son equivalentes respectivamente a los ejemplos a, b y c del punto 5.
6) Más ejemplos:
a) Podemos tomar también tres copias de N y tener así el ordenamiento 0, 1, 2, 3, 4,..., 0’, 1’, 2’, 3’, 4’,..., 0”, 1”, 2”, 3”, 4”,...
b) O podemos tomar infinitas copias de N, así: 0, 1, 2, 3, 4,..., 0’, 1’, 2’, 3’, 4’,..., 0”, 1”, 2”, 3”, 4”,..., 0”’, 1”’, 2”’, 3”’, 4”’,..., 0””, 1””, 2””, 3””, 4””,..., y así sucesivamente copia tras copia.
7) Todos los ordenamientos mostrados más arriba son buenos órdenes sobre los conjuntos respectivos.
8) En un conjunto finito hay esencialmente un único buen orden: se elige un elemento cualquiera como mínimo, otro como el siguiente del mínimo, otro como el siguiente de éste y así sucesivamente hasta agotar el conjunto.
9) La clase de equivalencia de un conjunto bien ordenado es la familia formada por todos los conjuntos equivalentes a él. Así por ejemplo, en la clase de equivalencia de N (considerado con su orden usual) está el conjunto d del punto 4 (cada conjunto debe tomarse con su orden), también está el conjunto a del punto 5 y también el conjunto X definido en el ejemplo 8 de la parte 3.
10) Definición: Se llama ordinal a la clase de equivalencia de un conjunto bien ordenado.
11) Nombre: Llamamos $\omega $ al ordinal que corresponde a N con su orden usual. En otras palabras, $\omega $ es el nombre de la clase de equivalencia de N (con su orden usual).
12) Más nombres:
0 es el ordinal del conjunto vacío.
1 es el ordinal de un conjunto de un elemento.
2 es el ordinal de un conjunto de dos elementos.
3 es el ordinal de un conjunto de tres elementos.
etc.
(En los conjuntos finitos no es necesario aclarar qué orden se usa pues, como ya dijimos en la parte anterior, todos los buenos órdenes en un conjunto finito son equivalentes.)
13) Más ordinales: el ordinal de 0, 1, 2, 3,..., 0’ es $\omega +1$ (pues a un conjunto de tipo $\omega $ le estamos agregando un elemento más "a su derecha").
El ordinal de 0, 1, 2, 3,..., 0’, 1’ es $\omega +2$.
El ordinal de 0, 1, 2, 3,..., 0’, 1’, 2’ es $\omega +3$.
El ordinal de 0, 1, 2, 3,..., 0’, 1’, 2’,... es $\omega +\omega $ (pues a un conjunto de tipo $\omega $ le agregamos otro de tipo $\omega $ a su derecha).
El ordinal de 0, 1, 2, 3, 4,..., 0’, 1’, 2’, 3’, 4’,..., 0”, 1”, 2”, 3”, 4”,..., 0”’, 1”’, 2”’, 3”’, 4”’,..., 0””, 1””, 2””, 3””, 4””,..., y así sucesivamente copia tras copia de N es $\omega +\omega +\omega+\dots $ infinitas veces.
Notas:
(1) Cantor establece una tercera regla para la formación de los ordinales, que es en realidad una regla de restricción que dice que a veces no es posible aplicar la regla 2. Esta tercera regla se relaciona con las paradojas que aparecieron luego y, dado que hablaremos de esas paradojas en entradas subsiguientes, no nos detendremos ahora a formular la regla con más precisión.
(2) En 1897 Cantor da una definición de conjunto bien ordenado que es diferente que la hemos dado nosotros (la nuestra es la definición usual hoy en día). La definición que da Cantor se relaciona con las dos primeras reglas de formación de ordinales. Para Cantor un conjunto F es bien ordenado si tiene un primer elemento y si dada cualquier sucesión creciente que no contenga al último elemento de F (si es que existe) entonces existe un primer elemento de F que es mayor que toda la sucesión. Inmediatamente después de dar esta definición Cantor demuestra que es equivalente a decir que todo subconjunto no vacío de F tiene primer elemento.
(A la parte 4 – A la parte 6)
28.11.07
El Omegón y todo eso... (Parte 4)
(A la parte 3 - A la parte 5)
Diferentes órdenes
Cuando en la entrada anterior hablábamos de N = {0, 1, 2, 3,...} pudo quedar la impresión de que en este conjunto existe un único ordenamiento posible. Es cierto que hay un orden "natural" o "usual" en el que, de menor a mayor, el ordenamiento es 0, 1, 2, 3,... Pero no es éste el único orden posible en N.
Por ejemplo, podríamos decidir arbitrariamente que el 0 es mayor que todos los números y que los demás se comparan entre sí de la manera usual. Así, de menor a mayor el orden es 1, 2, 3, 4,..., 0 (los puntos suspensivos abarcan todos infinitos números enteros mayores que 4). Con este nuevo orden N resulta ser, también, bien ordenado y es, de hecho, equivalente al conjunto Y mencionado en la parte anterior.
También podríamos decidir que los números impares se comparen entre sí de la manera usual, los pares se comparen entre sí de la manera usual, pero que cada impar es menor que cada par. De este modo el ordenamiento, de menor a mayor, es: 1, 3, 5, 7,... , 0, 2, 4, 6, 8,... (los primeros puntos suspensivos abarcan todos los impares mayores que 7, los segundos puntos suspensivos abarcan todos los pares mayores que 8). Con este orden N resulta ser también bien ordenado, pero este orden no es equivalente a ninguno de los vistos en la parte anterior.
Ejercicio para el lector interesado: Demostrar que N con el orden 1, 3, 5, 7,... , 0, 2, 4, 6, 8,... es bien ordenado.
El conjunto R de los números reales, con su orden usual, no es bien ordenado. ¿Es posible definir en R un orden (distinto del usual, claro está) para el cual R sí resulte bien ordenado? Más en general, dado un conjunto cualquiera ¿es posible definir en él un orden para que resulte bien ordenado? Cantor dio por supuesto que sí, aunque nunca dio una demostración formal del hecho; el primero en darla fue Ernst Zermelo, en 1904. En esta demostración Zermelo introdujo explícitamente por primera vez el axioma de elección, que en su momento generó gran controversia. (Las controversias en torno al axioma de elección serán tema de otras entradas.)
Ejercicio para el lector interesado: Si A es un conjunto finito, demostrar que existe en A un único buen orden. Es decir, si definimos en A dos órdenes para los cuales A resulta bien ordenado entonces esos órdenes son equivalentes. (La "filosofía" de este ejercicio es que existen muchas formas diferentes -por "diferentes" entendemos "no equivalentes"- de ordenar N de modo tal que resulte bien ordenado; en cambio para un conjunto finito existe esencialmente una única forma de ordenarlo de modo que resulte bien ordenado.)
Nota histórica:
El breve artículo en el que Zermelo demuestra el principio de buena ordenación fue originalmente parte de una carta escrita a David Hilbert fechada el 24 de septiembre de 1904. Cantor, en 1883, había conjeturado que todo conjunto podía ser bien ordenado y, aunque muchas veces anunció haber demostrado la conjetura, en todos los casos debió después retractarse de su anuncio. En el Tercer Congreso Internacional de Matemáticas, en 1904, J. König exhibió la que él consideraba una demostración de que R (el conjunto de los números reales) no podía ser bien ordenado, pero poco después reconoció que su demostración tenía errores. Pocos meses después del Tercer Congreso, Zermelo completó su demostración de la existencia de un buen orden para cualquier conjunto. En su demostración Zermelo hace explícito por primera vez el axioma de elección, que ya había sido implícitamente usado por otros matemáticos con anterioridad. (Datos extraídos de "From Frege to Gödel", Jean van Heijenoort, Harvard University Press, 1967.)
(A la parte 3 - A la parte 5)
Diferentes órdenes
Cuando en la entrada anterior hablábamos de N = {0, 1, 2, 3,...} pudo quedar la impresión de que en este conjunto existe un único ordenamiento posible. Es cierto que hay un orden "natural" o "usual" en el que, de menor a mayor, el ordenamiento es 0, 1, 2, 3,... Pero no es éste el único orden posible en N.
Por ejemplo, podríamos decidir arbitrariamente que el 0 es mayor que todos los números y que los demás se comparan entre sí de la manera usual. Así, de menor a mayor el orden es 1, 2, 3, 4,..., 0 (los puntos suspensivos abarcan todos infinitos números enteros mayores que 4). Con este nuevo orden N resulta ser, también, bien ordenado y es, de hecho, equivalente al conjunto Y mencionado en la parte anterior.
También podríamos decidir que los números impares se comparen entre sí de la manera usual, los pares se comparen entre sí de la manera usual, pero que cada impar es menor que cada par. De este modo el ordenamiento, de menor a mayor, es: 1, 3, 5, 7,... , 0, 2, 4, 6, 8,... (los primeros puntos suspensivos abarcan todos los impares mayores que 7, los segundos puntos suspensivos abarcan todos los pares mayores que 8). Con este orden N resulta ser también bien ordenado, pero este orden no es equivalente a ninguno de los vistos en la parte anterior.
Ejercicio para el lector interesado: Demostrar que N con el orden 1, 3, 5, 7,... , 0, 2, 4, 6, 8,... es bien ordenado.
El conjunto R de los números reales, con su orden usual, no es bien ordenado. ¿Es posible definir en R un orden (distinto del usual, claro está) para el cual R sí resulte bien ordenado? Más en general, dado un conjunto cualquiera ¿es posible definir en él un orden para que resulte bien ordenado? Cantor dio por supuesto que sí, aunque nunca dio una demostración formal del hecho; el primero en darla fue Ernst Zermelo, en 1904. En esta demostración Zermelo introdujo explícitamente por primera vez el axioma de elección, que en su momento generó gran controversia. (Las controversias en torno al axioma de elección serán tema de otras entradas.)
Ejercicio para el lector interesado: Si A es un conjunto finito, demostrar que existe en A un único buen orden. Es decir, si definimos en A dos órdenes para los cuales A resulta bien ordenado entonces esos órdenes son equivalentes. (La "filosofía" de este ejercicio es que existen muchas formas diferentes -por "diferentes" entendemos "no equivalentes"- de ordenar N de modo tal que resulte bien ordenado; en cambio para un conjunto finito existe esencialmente una única forma de ordenarlo de modo que resulte bien ordenado.)
Nota histórica:
El breve artículo en el que Zermelo demuestra el principio de buena ordenación fue originalmente parte de una carta escrita a David Hilbert fechada el 24 de septiembre de 1904. Cantor, en 1883, había conjeturado que todo conjunto podía ser bien ordenado y, aunque muchas veces anunció haber demostrado la conjetura, en todos los casos debió después retractarse de su anuncio. En el Tercer Congreso Internacional de Matemáticas, en 1904, J. König exhibió la que él consideraba una demostración de que R (el conjunto de los números reales) no podía ser bien ordenado, pero poco después reconoció que su demostración tenía errores. Pocos meses después del Tercer Congreso, Zermelo completó su demostración de la existencia de un buen orden para cualquier conjunto. En su demostración Zermelo hace explícito por primera vez el axioma de elección, que ya había sido implícitamente usado por otros matemáticos con anterioridad. (Datos extraídos de "From Frege to Gödel", Jean van Heijenoort, Harvard University Press, 1967.)
(A la parte 3 - A la parte 5)
El Omegón y todo eso... (Parte 3)
(A la parte 2 – A la parte 4)
Conjuntos bien ordenados
Como veremos en breve, la definición del concepto de ordinal que da Cantor en 1895/97 está estrechamente relacionada con la noción de conjunto bien ordenado, por lo que comenzaremos definiendo esta idea.
Definición: una relación de orden en un conjunto A es cualquier relación “$\leq $;” que cumpla estas dos condiciones:
a) Si $a\leq b$ y $b\leq c$ entonces $a\leq c$.
b) Para todo $a\in A$, $a \leq a$.
c) Si $a\leq b$ y $b \leq a$ entonces $a = b$.
Ejemplos:
1) Tomemos como A la familia de todos los subconjuntos de N = {0, 1, 2, 3,...} y la inclusión como relación, es decir, $U\leq V$ si U está contenido o es igual a V (donde U y V son subconjuntos cualesquiera de N). Es fácil ver que (A, $\leq $) es un conjunto ordenado.
2) El conjunto R de todos los números reales con su relación habitual de orden es, por supuesto, un conjunto ordenado.
En el segundo ejemplo, la relación cumple una propiedad adicional: para todo a, b sucede que $a\leq b$ o $b\leq a$. Cuando esto sucede se dice que el orden es total o lineal. En el primer ejemplo esto no sucede pues dados dos subconjuntos de N no necesariamente se cumple que uno de ellos esté contenido en el otro.
Definición: Si (A, $\leq $) es un conjunto ordenado y B es un subconjunto de A decimos que B tiene mínimo (o primer elemento) si existe algún $m\in B$ tal que $m\leq b$ para todo $b\in B$.
Ejemplos:
3) En R, el conjunto de todos los números reales, el intervalo [0, 1] (que es el conjunto de todos los números entre 0 y 1, incluyendo a ambos) tiene mínimo y es, obviamente, m = 0. El intervalo (0, 1) (que es el anterior, sin incluir al 0 ni al 1) no tiene mínimo. El propio R no tiene mínimo.
Definición: un conjunto (A, $\leq $) es bien ordenado si todo subconjunto no vacío de A tiene mínimo.
Ejercicio para el lector: Si (A, $\leq $) es bien ordenado entonces el orden en A es lineal.
Ejemplos:
4) R no es bien ordenado, pues, como vimos en el ejemplo anterior, existen subconjuntos de R que no tienen mínimo.
5) N = {0, 1, 2, 3,...}, el conjunto de los números naturales, es bien ordenado.
La demostración de esta afirmación se hace por inducción (1). Se toma como P(n) la siguiente afirmación: “si B es un subconjunto de N que contiene al número n entonces B tiene mínimo”. P(0) es la afirmación “si B es un subconjunto de N que contiene al 0 entonces B tiene mínimo”, esto es verdad porque si 0 está en B entonces el mismo 0 es el mínimo de B.
Supuesta la verdad de P(n) hay que probar la de P(n + 1). Supongamos que B contiene a n + 1. S B también contiene a n entonces B tiene mínimo por la suposición de que P(n) es verdadera. Si B no contiene a n, sea C el conjunto que se obtiene agregándole a B el número n. Por la suposición, C tiene mínimo. Si el mínimo de C es menor que n entonces es fácil ver que ese mismo número es mínimo de B. Si el mínimo de C es n entonces es fácil ver que el mínimo de B es n + 1. En cualquier caso, B tiene mínimo, como queríamos probar.
6) El conjunto vacío es bien ordenado. (Y quien no me crea, trate de encontrar un subconjunto no vacío que no tenga mínimo.)
7) Todo subconjunto finito de R es bien ordenado.
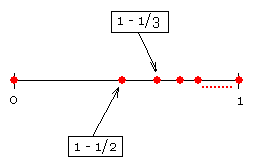
8) Sea X = {0, $1-\frac{1}{2}$, $1-\frac{1}{3}$, $1-\frac{1}{4}$,...}. Es decir X es el conjunto de todos los números de la forma $1-\frac{1}{n+1}$ con n natural.
Tomando en X el orden usual resulta que (X, $\leq $) es un conjunto bien ordenado. Esto puede probarse de manera directa, pero tiene mucho interés para nosotros el siguiente razonamiento: sea $f:N\rightarrow X$ la función definida por f(n) = $1-\frac{1}{n+1}$. Es fácil ver que f es una función biyectiva ("empareja" perfectamente cada elemento de N con un elemento de X) tal que si $n\leq m$ entonces $f(n)\leq f(m)$.
Esta función f demuestra que el orden en X es una “copia textual” del orden en N. Como N es bien ordenado entonces X también.
9) Sea Y = {0, $1-\frac{1}{2}$, $1-\frac{1}{3}$, $1-\frac{1}{4}$,...}, es decir, el conjunto formado por todos los números de X y al que le agregamos además el 1. El orden en Y no "copia" el orden en N, ya que en Y existe un elemento que es mayor que todos los demás (el 1) mientras que en N eso no sucede, no obstante puede demostrarse que Y es un conjunto bien ordenado (la demostración queda como ejercicio para el lector interesado).
El ejemplo 8 motiva la siguiente definición (Cantor, 1895):
Definición: Dos conjuntos ordenados (A, $\leq _A$) y (B, $\leq _B$) son equivalentes (Cantor dice “similares”) si existe una función biyectiva $f :A\rightarrow B$ tal que si $a\leq _Ab$ entonces $f(a)\leq _Bf(b)$. En ese caso (A, $\leq _A$) y (B, $\leq _B$) tienen esencialmente el mismo ordenamiento.
Es bastante claro que la relación definida es una relación de equivalencia entre los conjuntos ordenados. A la clase de equivalencia de (A, $\leq _A$) (es decir, a la familia de todos los (B, $\leq _B$) que son equivalente a (A, $\leq _A$)) se lo llama el “tipo ordinal de (A, $\leq _A$)”. Así por ejemplo, (N, $\leq $) del ejemplo 5 y (X, $\leq $) del ejemplo 8 tienen el mismo tipo ordinal.
Adelantamos la siguiente definición, que será desarrollada en detalle en la próxima entrada:
Definición: “Número ordinal” es la clase de equivalencia de un conjunto bien ordenado.
Por ejemplo, la clase de equivalencia de (N, $\leq $) (que incluye, entre otros, a (X, $\leq $)) es un ordinal. A este ordinal (la nomenclatura es de Cantor) se lo suele llamar $\omega $ (léase “omega minúscula” u “omeguita”). Como el orden en (Y, $\leq $) no es una "copia" del de (N, $\leq $) entonces a (Y, $\leq $) le corresponde un ordinal diferente. Como veremos después, el ordinal de (Y, $\leq $) es $\omega + 1$.
Nota histórica:
Cantor define la noción de “tipo ordinal” en su artículo de 1895. Allí estudia el tipo ordinal de R (el conjunto de los números reales) y el de Q (el conjunto de los números racionales). En su artículo de 1897 define la noción de conjunto bien ordenado y la de número ordinal (de esta última definición ya había dado una versión más primitiva en 1883).
Pero Cantor no habla de clases de equivalencia, él dice que el tipo ordinal de A se obtiene haciendo abstracción de la naturaleza de los elementos de A pero conservando su ordenamiento. El tipo ordinal de A, para Cantor, es un conjunto formado por “unidades” ordenadas. La idea es más o menos así:
El tipo ordinal de N tendría este aspecto: * * * * .... (un primer elemento, luego otro, luego otro, etc.) El tipo ordinal de Y sería: * * * * .... * (como el de N pero agregando un elemento que es mayor que todos los demás). El tipo ordinal de un subconjunto finito de R que tenga tres elementos es: * * *.
La notación que Cantor usa para el tipo ordinal de A es la letra A con una rayita arriba. Esta rayita representaría el acto de abstraer la naturaleza de los elementos de A. En el artículo de 1895 Cantor define también la noción de cardinal (que se relaciona con la “cantidad de elementos de un conjunto” independientemente de su orden). Para Cantor el cardinal (que él llamaba potencia del conjunto) resulta de un segundo acto de abstracción, en el que, además de la naturaleza de los elementos, olvidamos su ordenamiento. La notación de Cantor para el cardinal de A es A con dos rayitas arriba, dos rayitas pues se obtiene por un doble acto de abstracción.
Nota:
(1) El principio de inducción dice que si P(n) es una propiedad referida a los números naturales tal que P(0) es verdadera y tal que de suponer la verdad de P(n) se puede deducir la verdad de P(n + 1) entonces P(n) es verdadera para todo n natural.
Conjuntos bien ordenados
Como veremos en breve, la definición del concepto de ordinal que da Cantor en 1895/97 está estrechamente relacionada con la noción de conjunto bien ordenado, por lo que comenzaremos definiendo esta idea.
Definición: una relación de orden en un conjunto A es cualquier relación “$\leq $;” que cumpla estas dos condiciones:
a) Si $a\leq b$ y $b\leq c$ entonces $a\leq c$.
b) Para todo $a\in A$, $a \leq a$.
c) Si $a\leq b$ y $b \leq a$ entonces $a = b$.
Ejemplos:
1) Tomemos como A la familia de todos los subconjuntos de N = {0, 1, 2, 3,...} y la inclusión como relación, es decir, $U\leq V$ si U está contenido o es igual a V (donde U y V son subconjuntos cualesquiera de N). Es fácil ver que (A, $\leq $) es un conjunto ordenado.
2) El conjunto R de todos los números reales con su relación habitual de orden es, por supuesto, un conjunto ordenado.
En el segundo ejemplo, la relación cumple una propiedad adicional: para todo a, b sucede que $a\leq b$ o $b\leq a$. Cuando esto sucede se dice que el orden es total o lineal. En el primer ejemplo esto no sucede pues dados dos subconjuntos de N no necesariamente se cumple que uno de ellos esté contenido en el otro.
Definición: Si (A, $\leq $) es un conjunto ordenado y B es un subconjunto de A decimos que B tiene mínimo (o primer elemento) si existe algún $m\in B$ tal que $m\leq b$ para todo $b\in B$.
Ejemplos:
3) En R, el conjunto de todos los números reales, el intervalo [0, 1] (que es el conjunto de todos los números entre 0 y 1, incluyendo a ambos) tiene mínimo y es, obviamente, m = 0. El intervalo (0, 1) (que es el anterior, sin incluir al 0 ni al 1) no tiene mínimo. El propio R no tiene mínimo.
Definición: un conjunto (A, $\leq $) es bien ordenado si todo subconjunto no vacío de A tiene mínimo.
Ejercicio para el lector: Si (A, $\leq $) es bien ordenado entonces el orden en A es lineal.
Ejemplos:
4) R no es bien ordenado, pues, como vimos en el ejemplo anterior, existen subconjuntos de R que no tienen mínimo.
5) N = {0, 1, 2, 3,...}, el conjunto de los números naturales, es bien ordenado.
La demostración de esta afirmación se hace por inducción (1). Se toma como P(n) la siguiente afirmación: “si B es un subconjunto de N que contiene al número n entonces B tiene mínimo”. P(0) es la afirmación “si B es un subconjunto de N que contiene al 0 entonces B tiene mínimo”, esto es verdad porque si 0 está en B entonces el mismo 0 es el mínimo de B.
Supuesta la verdad de P(n) hay que probar la de P(n + 1). Supongamos que B contiene a n + 1. S B también contiene a n entonces B tiene mínimo por la suposición de que P(n) es verdadera. Si B no contiene a n, sea C el conjunto que se obtiene agregándole a B el número n. Por la suposición, C tiene mínimo. Si el mínimo de C es menor que n entonces es fácil ver que ese mismo número es mínimo de B. Si el mínimo de C es n entonces es fácil ver que el mínimo de B es n + 1. En cualquier caso, B tiene mínimo, como queríamos probar.
6) El conjunto vacío es bien ordenado. (Y quien no me crea, trate de encontrar un subconjunto no vacío que no tenga mínimo.)
7) Todo subconjunto finito de R es bien ordenado.
8) Sea X = {0, $1-\frac{1}{2}$, $1-\frac{1}{3}$, $1-\frac{1}{4}$,...}. Es decir X es el conjunto de todos los números de la forma $1-\frac{1}{n+1}$ con n natural.
Tomando en X el orden usual resulta que (X, $\leq $) es un conjunto bien ordenado. Esto puede probarse de manera directa, pero tiene mucho interés para nosotros el siguiente razonamiento: sea $f:N\rightarrow X$ la función definida por f(n) = $1-\frac{1}{n+1}$. Es fácil ver que f es una función biyectiva ("empareja" perfectamente cada elemento de N con un elemento de X) tal que si $n\leq m$ entonces $f(n)\leq f(m)$.Esta función f demuestra que el orden en X es una “copia textual” del orden en N. Como N es bien ordenado entonces X también.9) Sea Y = {0, $1-\frac{1}{2}$, $1-\frac{1}{3}$, $1-\frac{1}{4}$,...}, es decir, el conjunto formado por todos los números de X y al que le agregamos además el 1. El orden en Y no "copia" el orden en N, ya que en Y existe un elemento que es mayor que todos los demás (el 1) mientras que en N eso no sucede, no obstante puede demostrarse que Y es un conjunto bien ordenado (la demostración queda como ejercicio para el lector interesado).
El ejemplo 8 motiva la siguiente definición (Cantor, 1895):Definición: Dos conjuntos ordenados (A, $\leq _A$) y (B, $\leq _B$) son equivalentes (Cantor dice “similares”) si existe una función biyectiva $f :A\rightarrow B$ tal que si $a\leq _Ab$ entonces $f(a)\leq _Bf(b)$. En ese caso (A, $\leq _A$) y (B, $\leq _B$) tienen esencialmente el mismo ordenamiento.
Es bastante claro que la relación definida es una relación de equivalencia entre los conjuntos ordenados. A la clase de equivalencia de (A, $\leq _A$) (es decir, a la familia de todos los (B, $\leq _B$) que son equivalente a (A, $\leq _A$)) se lo llama el “tipo ordinal de (A, $\leq _A$)”. Así por ejemplo, (N, $\leq $) del ejemplo 5 y (X, $\leq $) del ejemplo 8 tienen el mismo tipo ordinal.
Adelantamos la siguiente definición, que será desarrollada en detalle en la próxima entrada:
Definición: “Número ordinal” es la clase de equivalencia de un conjunto bien ordenado.
Por ejemplo, la clase de equivalencia de (N, $\leq $) (que incluye, entre otros, a (X, $\leq $)) es un ordinal. A este ordinal (la nomenclatura es de Cantor) se lo suele llamar $\omega $ (léase “omega minúscula” u “omeguita”). Como el orden en (Y, $\leq $) no es una "copia" del de (N, $\leq $) entonces a (Y, $\leq $) le corresponde un ordinal diferente. Como veremos después, el ordinal de (Y, $\leq $) es $\omega + 1$.
Nota histórica:
Cantor define la noción de “tipo ordinal” en su artículo de 1895. Allí estudia el tipo ordinal de R (el conjunto de los números reales) y el de Q (el conjunto de los números racionales). En su artículo de 1897 define la noción de conjunto bien ordenado y la de número ordinal (de esta última definición ya había dado una versión más primitiva en 1883).
Pero Cantor no habla de clases de equivalencia, él dice que el tipo ordinal de A se obtiene haciendo abstracción de la naturaleza de los elementos de A pero conservando su ordenamiento. El tipo ordinal de A, para Cantor, es un conjunto formado por “unidades” ordenadas. La idea es más o menos así:
El tipo ordinal de N tendría este aspecto: * * * * .... (un primer elemento, luego otro, luego otro, etc.) El tipo ordinal de Y sería: * * * * .... * (como el de N pero agregando un elemento que es mayor que todos los demás). El tipo ordinal de un subconjunto finito de R que tenga tres elementos es: * * *.
La notación que Cantor usa para el tipo ordinal de A es la letra A con una rayita arriba. Esta rayita representaría el acto de abstraer la naturaleza de los elementos de A. En el artículo de 1895 Cantor define también la noción de cardinal (que se relaciona con la “cantidad de elementos de un conjunto” independientemente de su orden). Para Cantor el cardinal (que él llamaba potencia del conjunto) resulta de un segundo acto de abstracción, en el que, además de la naturaleza de los elementos, olvidamos su ordenamiento. La notación de Cantor para el cardinal de A es A con dos rayitas arriba, dos rayitas pues se obtiene por un doble acto de abstracción.
Nota:
(1) El principio de inducción dice que si P(n) es una propiedad referida a los números naturales tal que P(0) es verdadera y tal que de suponer la verdad de P(n) se puede deducir la verdad de P(n + 1) entonces P(n) es verdadera para todo n natural.
22.11.07
El Omegón y todo eso... (Parte 2)
(A la parte 1 – A la parte 3)
Breve introducción histórica
Comenzaremos nuestra exposición con un breve resumen de la historia de los ordinales. Tómese este resumen como un índice de lo que vamos a ir desarrollando en las sucesivas entradas, una especie de esqueleto que, con el tiempo, iremos lentamente cubriendo de carne y sangre.
Como decíamos en otra ocasión (véase aquí) hay dos formas de concebir el infinito, la forma “potencial” y la forma “actual” (quien hizo esta distinción por primera vez fue Aristóteles). El infinito potencial, o en potencia, es un infinito que nunca llega a realizarse, se trata solamente de una cantidad finita que puede aumentarse tanto como se quiera, pero que nunca deja de ser finita. Por ejemplo, cuando Euclides, en sus Elementos, enuncia que hay infinitos números primos lo dice la siguiente forma: es posible aumentar (finitamente) cualquier cantidad (finita) dada de números primos. Es decir, la cantidad de primos conocidos es en todo momento finita, pero siempre puede aumentarse un poco más.
En contraposición, el infinito actual, o en acto, es un infinito que ya se ha alcanzado. Es una cantidad infinita de hecho. Cuando decimos “hay infinitos primos” e imaginamos a todos los primos juntos, existentes todos a la vez, estamos pensando en un infinito en acto.
Desde Aristóteles y hasta fines del siglo XIX los matemáticos sólo aceptaron como válida la concepción potencial del infinito y rechazaron unánimemente, como absurda y sin sentido, la idea del infinito en acto. Este rechazo provenía esencialmente de una visión realista de la matemática, una visión en la que la matemática debía reflejar inevitablemente la realidad física, en la cual el infinito, es verdad, sólo existe en forma potencial.
Quien rompió con este rechazo e introdujo el infinito actual en la matemática fue Georg Cantor. No fue fácil para él. De hecho, en 1883 Cantor escribió: “he sido llevado casi contra su voluntad, por la lógica de mis investigaciones, a romper con tradiciones que me habían enseñado a venerar” (por esas tradiciones se entiende el rechazo al infinito actual).
¿Qué investigaciones fueron ésas? Ya lo veremos con detalle más adelante. Baste decir por ahora que Cantor se topó con el primer atisbo de los ordinales (y con ellos del infinito actual, pues los ordinales son infinitos en acto) hacia 1872. Sin embargo, tan fuerte era en él el respeto a las tradiciones, que recién admitió la existencia de los ordinales (y su carácter infinito) en 1883, en un artículo donde no sólo defendió su existencia, sino que los definió por primera vez y expuso algunas de sus propiedades. Es en ese artículo de 1883 donde aparece la frase citada más arriba.
Hacia 1884 Cantor sufre un colapso nervioso. Contribuyen a él muchos factores, entre ellos el pertinaz rechazo que muchos matemáticos influyentes habían venido mostrando hacia su trabajo (no es fácil romper con veneradas tradiciones) y una pelea con Richard Dedekind, uno de sus amigos más íntimos a la vez que uno de sus más firmes defensores. Después de este colapso Cantor abandona la matemática durante varios años.
Hacia 1893 una nueva generación de matemáticos (entre los que se destaca David Hilbert) asciende a puestos de poder. Esta generación (como en toda generación nueva) está más dispuesta a romper con viejas tradiciones y acepta de buen grado la teoría de Cantor. Éste, entonces, se reconcilia con sus colegas y vuelve al trabajo. En 1895 y 1897 publica sendos artículos sobre su teoría de los ordinales y los cardinales. En el primero de estos artículos, entre muchas otras cosas, da una definición más precisa de la noción de ordinal (y también de cardinal). En el segundo profundiza el estudio de los ordinales y los cardinales. (Es en el artículo de 1895 donde aparecen por primera vez los famosos aleph.)
Cantor tenía la intención de publicar un tercer artículo en 1899, pero antes de completarlo sufre un nuevo colapso nervioso (producido en este caso por la muerte de su hijo menor) del cual ya nunca se recuperaría. Cantor murió en 1918.
Entre 1895 y 1902 se descubren varias paradojas (léase contradicciones o incoherencias) en la teoría de Cantor. Las primeras las encuentra el propio Cantor (aunque una suele atribuirse erróneamente a Césare Burali-Forti), la última la encuentra Bertrand Russell. Con el tiempo, estas paradojas obligaron a una reformulación de toda la teoría de Cantor, la cual quedó finalmente contendida en la teoría axiomática de conjuntos de Zermelo-Fraenkel (ZF). Esta teoría axiomática fue formulada originalmente por Ernst Zermelo en 1908 y fue modificada en los años subsiguientes por varios matemáticos, entre ellos Fraenkel, Bernays, von Neumann, etc. Fue precisamente John von Neumann en 1923 quien dio la definición moderna, siempre en el contexto de ZF, de la noción de ordinal, definición que siguen usando actualmente los matemáticos, o al menos los matemáticos que se ocupan de estas cosas.
Comenzaremos a cubrir este esqueleto por el año 1895. En nuestra próxima entrada desarrollaremos, traducida a un lenguaje moderno, la definición de ordinal que Cantor dio en su artículo de ese año.
(A la parte 1 – A la parte 3)
Breve introducción histórica
Comenzaremos nuestra exposición con un breve resumen de la historia de los ordinales. Tómese este resumen como un índice de lo que vamos a ir desarrollando en las sucesivas entradas, una especie de esqueleto que, con el tiempo, iremos lentamente cubriendo de carne y sangre.
Como decíamos en otra ocasión (véase aquí) hay dos formas de concebir el infinito, la forma “potencial” y la forma “actual” (quien hizo esta distinción por primera vez fue Aristóteles). El infinito potencial, o en potencia, es un infinito que nunca llega a realizarse, se trata solamente de una cantidad finita que puede aumentarse tanto como se quiera, pero que nunca deja de ser finita. Por ejemplo, cuando Euclides, en sus Elementos, enuncia que hay infinitos números primos lo dice la siguiente forma: es posible aumentar (finitamente) cualquier cantidad (finita) dada de números primos. Es decir, la cantidad de primos conocidos es en todo momento finita, pero siempre puede aumentarse un poco más.
En contraposición, el infinito actual, o en acto, es un infinito que ya se ha alcanzado. Es una cantidad infinita de hecho. Cuando decimos “hay infinitos primos” e imaginamos a todos los primos juntos, existentes todos a la vez, estamos pensando en un infinito en acto.
Desde Aristóteles y hasta fines del siglo XIX los matemáticos sólo aceptaron como válida la concepción potencial del infinito y rechazaron unánimemente, como absurda y sin sentido, la idea del infinito en acto. Este rechazo provenía esencialmente de una visión realista de la matemática, una visión en la que la matemática debía reflejar inevitablemente la realidad física, en la cual el infinito, es verdad, sólo existe en forma potencial.
Quien rompió con este rechazo e introdujo el infinito actual en la matemática fue Georg Cantor. No fue fácil para él. De hecho, en 1883 Cantor escribió: “he sido llevado casi contra su voluntad, por la lógica de mis investigaciones, a romper con tradiciones que me habían enseñado a venerar” (por esas tradiciones se entiende el rechazo al infinito actual).
¿Qué investigaciones fueron ésas? Ya lo veremos con detalle más adelante. Baste decir por ahora que Cantor se topó con el primer atisbo de los ordinales (y con ellos del infinito actual, pues los ordinales son infinitos en acto) hacia 1872. Sin embargo, tan fuerte era en él el respeto a las tradiciones, que recién admitió la existencia de los ordinales (y su carácter infinito) en 1883, en un artículo donde no sólo defendió su existencia, sino que los definió por primera vez y expuso algunas de sus propiedades. Es en ese artículo de 1883 donde aparece la frase citada más arriba.
Hacia 1884 Cantor sufre un colapso nervioso. Contribuyen a él muchos factores, entre ellos el pertinaz rechazo que muchos matemáticos influyentes habían venido mostrando hacia su trabajo (no es fácil romper con veneradas tradiciones) y una pelea con Richard Dedekind, uno de sus amigos más íntimos a la vez que uno de sus más firmes defensores. Después de este colapso Cantor abandona la matemática durante varios años.
Hacia 1893 una nueva generación de matemáticos (entre los que se destaca David Hilbert) asciende a puestos de poder. Esta generación (como en toda generación nueva) está más dispuesta a romper con viejas tradiciones y acepta de buen grado la teoría de Cantor. Éste, entonces, se reconcilia con sus colegas y vuelve al trabajo. En 1895 y 1897 publica sendos artículos sobre su teoría de los ordinales y los cardinales. En el primero de estos artículos, entre muchas otras cosas, da una definición más precisa de la noción de ordinal (y también de cardinal). En el segundo profundiza el estudio de los ordinales y los cardinales. (Es en el artículo de 1895 donde aparecen por primera vez los famosos aleph.)
Cantor tenía la intención de publicar un tercer artículo en 1899, pero antes de completarlo sufre un nuevo colapso nervioso (producido en este caso por la muerte de su hijo menor) del cual ya nunca se recuperaría. Cantor murió en 1918.
Entre 1895 y 1902 se descubren varias paradojas (léase contradicciones o incoherencias) en la teoría de Cantor. Las primeras las encuentra el propio Cantor (aunque una suele atribuirse erróneamente a Césare Burali-Forti), la última la encuentra Bertrand Russell. Con el tiempo, estas paradojas obligaron a una reformulación de toda la teoría de Cantor, la cual quedó finalmente contendida en la teoría axiomática de conjuntos de Zermelo-Fraenkel (ZF). Esta teoría axiomática fue formulada originalmente por Ernst Zermelo en 1908 y fue modificada en los años subsiguientes por varios matemáticos, entre ellos Fraenkel, Bernays, von Neumann, etc. Fue precisamente John von Neumann en 1923 quien dio la definición moderna, siempre en el contexto de ZF, de la noción de ordinal, definición que siguen usando actualmente los matemáticos, o al menos los matemáticos que se ocupan de estas cosas.
Comenzaremos a cubrir este esqueleto por el año 1895. En nuestra próxima entrada desarrollaremos, traducida a un lenguaje moderno, la definición de ordinal que Cantor dio en su artículo de ese año.
(A la parte 1 – A la parte 3)
21.11.07
El Omegón y todo eso... (Parte 1)
(A la parte 2)
Introducción
La teoría de los transfinitos de Georg Cantor involucra principalmente dos conceptos: la noción de cardinal de un conjunto y la noción de ordinal de un conjunto. De estas dos nociones, la de los cardinales es la más conocida; los legendarios $\aleph_0$, $\aleph_1$,... son cardinales y es también dentro del contexto del concepto de cardinal que se enuncia la famosa Hipótesis del Continuo (1). Los ordinales, por el contrario, han sido tal vez menos difundidos y es probable que muchos de quienes conocen la existencia de los famosos $\aleph $ casi no hayan oído hablar, por ejemplo, del Omegón ($\Omega $), el primer ordinal no numerable.
Nuestra intención es ofrecer, en una serie de entradas, una introducción a la teoría de los ordinales, que contemple su definición, sus propiedades, su evolución histórica y algunas de sus aplicaciones.
Nota:
(1) De los aleph y de la Hipótesis del Continuo hablaremos también a lo largo de estas entradas.
(A la parte 2)
Introducción
La teoría de los transfinitos de Georg Cantor involucra principalmente dos conceptos: la noción de cardinal de un conjunto y la noción de ordinal de un conjunto. De estas dos nociones, la de los cardinales es la más conocida; los legendarios $\aleph_0$, $\aleph_1$,... son cardinales y es también dentro del contexto del concepto de cardinal que se enuncia la famosa Hipótesis del Continuo (1). Los ordinales, por el contrario, han sido tal vez menos difundidos y es probable que muchos de quienes conocen la existencia de los famosos $\aleph $ casi no hayan oído hablar, por ejemplo, del Omegón ($\Omega $), el primer ordinal no numerable.
Nuestra intención es ofrecer, en una serie de entradas, una introducción a la teoría de los ordinales, que contemple su definición, sus propiedades, su evolución histórica y algunas de sus aplicaciones.
Nota:
(1) De los aleph y de la Hipótesis del Continuo hablaremos también a lo largo de estas entradas.
(A la parte 2)
1.11.07
Un problema de lógica
En una habitación hay tres personajes, llamados Alfio, Beto y Gamo. Algunos (tal vez todos, tal vez ninguno) son veraces: todas sus afirmaciones son verdaderas. Otros (tal vez todos, tal vez ninguno) son mentirosos: todas sus afirmaciones son falsas. Ninguno de los tres se conocía a los otros antes de llegar a la habitación por lo que nadie sabe cuáles de los otros dos son veraces o mentirosos.
Una caja en la habitación contiene (y los nuestros tres protagonistas lo saben) cinco sombreros, tres de los cuales son blancos y dos son negros. Con los ojos cerrados, cada uno de los tres toma un sombrero y se lo pone en la cabeza. La caja después es cerrada de modo que nadie sepa qué sombreros quedaron dentro.
Después de ponerse los sombreros, al abrir los ojos, cada uno conoce qué sombreros tienen los otros, pero no el propio (no hay espejos ni otras superficies reflectantes, no hay trampa).
Después de un rato Alfio dice: "Puedo deducir de qué color es mi sombrero".
(Una aclaración necesaria: los tres son lógicos perfectos. Si Alfio dice que puede deducir el color de su sombrero es que la información de que dispone es suficiente como para hacer esa deducción. Claro que Alfio puede estar mintiendo al afirmar eso. Por cierto, la información de que dispone Alfio es la que aquí se ha dicho, además del hecho de que él puede ver el color del sombrero de Beto y Gamo.)
Beto agrega: "Veo dos sombreros del mismo color."
Gamo dice entonces: "Puedo deducir si Beto es veraz o mentiroso".
Alfio agrega: "Puedo deducir si Gamo es veraz o mentiroso."
Beto dice entonces: "Puedo deducir el color de mi sombrero."
¿De qué color es el sombrero de cada uno? ¿Quénes son veraces y quiénes son mentirosos?
Una caja en la habitación contiene (y los nuestros tres protagonistas lo saben) cinco sombreros, tres de los cuales son blancos y dos son negros. Con los ojos cerrados, cada uno de los tres toma un sombrero y se lo pone en la cabeza. La caja después es cerrada de modo que nadie sepa qué sombreros quedaron dentro.
Después de ponerse los sombreros, al abrir los ojos, cada uno conoce qué sombreros tienen los otros, pero no el propio (no hay espejos ni otras superficies reflectantes, no hay trampa).
Después de un rato Alfio dice: "Puedo deducir de qué color es mi sombrero".
(Una aclaración necesaria: los tres son lógicos perfectos. Si Alfio dice que puede deducir el color de su sombrero es que la información de que dispone es suficiente como para hacer esa deducción. Claro que Alfio puede estar mintiendo al afirmar eso. Por cierto, la información de que dispone Alfio es la que aquí se ha dicho, además del hecho de que él puede ver el color del sombrero de Beto y Gamo.)
Beto agrega: "Veo dos sombreros del mismo color."
Gamo dice entonces: "Puedo deducir si Beto es veraz o mentiroso".
Alfio agrega: "Puedo deducir si Gamo es veraz o mentiroso."
Beto dice entonces: "Puedo deducir el color de mi sombrero."
¿De qué color es el sombrero de cada uno? ¿Quénes son veraces y quiénes son mentirosos?
Suscribirse a:
Entradas (Atom)