El Omegón y todo eso... (Parte 3)

(A la parte 2 – A la parte 4)

Conjuntos bien ordenados

Como veremos en breve, la definición del concepto de ordinal que da Cantor en 1895/97 está estrechamente relacionada con la noción de conjunto bien ordenado, por lo que comenzaremos definiendo esta idea.

Definición: una relación de orden en un conjunto A es cualquier relación “$\leq $;” que cumpla estas dos condiciones:

a) Si $a\leq b$ y $b\leq c$ entonces $a\leq c$.
b) Para todo $a\in A$, $a \leq a$.
c) Si $a\leq b$ y $b \leq a$ entonces $a = b$.

Ejemplos:

1) Tomemos como A la familia de todos los subconjuntos de N = {0, 1, 2, 3,...} y la inclusión como relación, es decir, $U\leq V$ si U está contenido o es igual a V (donde U y V son subconjuntos cualesquiera de N). Es fácil ver que (A, $\leq $) es un conjunto ordenado.

2) El conjunto R de todos los números reales con su relación habitual de orden es, por supuesto, un conjunto ordenado.

En el segundo ejemplo, la relación cumple una propiedad adicional: para todo a, b sucede que $a\leq b$ o $b\leq a$. Cuando esto sucede se dice que el orden es total o lineal. En el primer ejemplo esto no sucede pues dados dos subconjuntos de N no necesariamente se cumple que uno de ellos esté contenido en el otro.

Definición: Si (A, $\leq $) es un conjunto ordenado y B es un subconjunto de A decimos que B tiene mínimo (o primer elemento) si existe algún $m\in B$ tal que $m\leq b$ para todo $b\in B$.

Ejemplos:

3) En R, el conjunto de todos los números reales, el intervalo [0, 1] (que es el conjunto de todos los números entre 0 y 1, incluyendo a ambos) tiene mínimo y es, obviamente, m = 0. El intervalo (0, 1) (que es el anterior, sin incluir al 0 ni al 1) no tiene mínimo. El propio R no tiene mínimo.

Definición: un conjunto (A, $\leq $) es bien ordenado si todo subconjunto no vacío de A tiene mínimo.

Ejercicio para el lector: Si (A, $\leq $) es bien ordenado entonces el orden en A es lineal.

Ejemplos:

4) R no es bien ordenado, pues, como vimos en el ejemplo anterior, existen subconjuntos de R que no tienen mínimo.

5) N = {0, 1, 2, 3,...}, el conjunto de los números naturales, es bien ordenado.

La demostración de esta afirmación se hace por inducción (1). Se toma como P(n) la siguiente afirmación: “si B es un subconjunto de N que contiene al número n entonces B tiene mínimo”. P(0) es la afirmación “si B es un subconjunto de N que contiene al 0 entonces B tiene mínimo”, esto es verdad porque si 0 está en B entonces el mismo 0 es el mínimo de B.

Supuesta la verdad de P(n) hay que probar la de P(n + 1). Supongamos que B contiene a n + 1. S B también contiene a n entonces B tiene mínimo por la suposición de que P(n) es verdadera. Si B no contiene a n, sea C el conjunto que se obtiene agregándole a B el número n. Por la suposición, C tiene mínimo. Si el mínimo de C es menor que n entonces es fácil ver que ese mismo número es mínimo de B. Si el mínimo de C es n entonces es fácil ver que el mínimo de B es n + 1. En cualquier caso, B tiene mínimo, como queríamos probar.

6) El conjunto vacío es bien ordenado. (Y quien no me crea, trate de encontrar un subconjunto no vacío que no tenga mínimo.)

7) Todo subconjunto finito de R es bien ordenado.

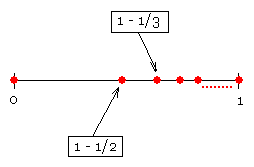
8) Sea X = {0, $1-\frac{1}{2}$, $1-\frac{1}{3}$, $1-\frac{1}{4}$,...}. Es decir X es el conjunto de todos los números de la forma $1-\frac{1}{n+1}$ con n natural.

Tomando en X el orden usual resulta que (X, $\leq $) es un conjunto bien ordenado. Esto puede probarse de manera directa, pero tiene mucho interés para nosotros el siguiente razonamiento: sea $f:N\rightarrow X$ la función definida por f(n) = $1-\frac{1}{n+1}$. Es fácil ver que f es una función biyectiva ("empareja" perfectamente cada elemento de N con un elemento de X) tal que si $n\leq m$ entonces $f(n)\leq f(m)$.
Esta función f demuestra que el orden en X es una “copia textual” del orden en N. Como N es bien ordenado entonces X también.

9) Sea Y = {0, $1-\frac{1}{2}$, $1-\frac{1}{3}$, $1-\frac{1}{4}$,...}, es decir, el conjunto formado por todos los números de X y al que le agregamos además el 1. El orden en Y no "copia" el orden en N, ya que en Y existe un elemento que es mayor que todos los demás (el 1) mientras que en N eso no sucede, no obstante puede demostrarse que Y es un conjunto bien ordenado (la demostración queda como ejercicio para el lector interesado).
El ejemplo 8 motiva la siguiente definición (Cantor, 1895):

Definición: Dos conjuntos ordenados (A, $\leq _A$) y (B, $\leq _B$) son equivalentes (Cantor dice “similares”) si existe una función biyectiva $f :A\rightarrow B$ tal que si $a\leq _Ab$ entonces $f(a)\leq _Bf(b)$. En ese caso (A, $\leq _A$) y (B, $\leq _B$) tienen esencialmente el mismo ordenamiento.

Es bastante claro que la relación definida es una relación de equivalencia entre los conjuntos ordenados. A la clase de equivalencia de (A, $\leq _A$) (es decir, a la familia de todos los (B, $\leq _B$) que son equivalente a (A, $\leq _A$)) se lo llama el “tipo ordinal de (A, $\leq _A$)”. Así por ejemplo, (N, $\leq $) del ejemplo 5 y (X, $\leq $) del ejemplo 8 tienen el mismo tipo ordinal.

Adelantamos la siguiente definición, que será desarrollada en detalle en la próxima entrada:

Definición: “Número ordinal” es la clase de equivalencia de un conjunto bien ordenado.

Por ejemplo, la clase de equivalencia de (N, $\leq $) (que incluye, entre otros, a (X, $\leq $)) es un ordinal. A este ordinal (la nomenclatura es de Cantor) se lo suele llamar $\omega $ (léase “omega minúscula” u “omeguita”). Como el orden en (Y, $\leq $) no es una "copia" del de (N, $\leq $) entonces a (Y, $\leq $) le corresponde un ordinal diferente. Como veremos después, el ordinal de (Y, $\leq $) es $\omega + 1$.

Nota histórica:
Cantor define la noción de “tipo ordinal” en su artículo de 1895. Allí estudia el tipo ordinal de R (el conjunto de los números reales) y el de Q (el conjunto de los números racionales). En su artículo de 1897 define la noción de conjunto bien ordenado y la de número ordinal (de esta última definición ya había dado una versión más primitiva en 1883).

Pero Cantor no habla de clases de equivalencia, él dice que el tipo ordinal de A se obtiene haciendo abstracción de la naturaleza de los elementos de A pero conservando su ordenamiento. El tipo ordinal de A, para Cantor, es un conjunto formado por “unidades” ordenadas. La idea es más o menos así:

El tipo ordinal de N tendría este aspecto: * * * * .... (un primer elemento, luego otro, luego otro, etc.) El tipo ordinal de Y sería: * * * * .... * (como el de N pero agregando un elemento que es mayor que todos los demás). El tipo ordinal de un subconjunto finito de R que tenga tres elementos es: * * *.

La notación que Cantor usa para el tipo ordinal de A es la letra A con una rayita arriba. Esta rayita representaría el acto de abstraer la naturaleza de los elementos de A. En el artículo de 1895 Cantor define también la noción de cardinal (que se relaciona con la “cantidad de elementos de un conjunto” independientemente de su orden). Para Cantor el cardinal (que él llamaba potencia del conjunto) resulta de un segundo acto de abstracción, en el que, además de la naturaleza de los elementos, olvidamos su ordenamiento. La notación de Cantor para el cardinal de A es A con dos rayitas arriba, dos rayitas pues se obtiene por un doble acto de abstracción.

Nota:

(1) El principio de inducción dice que si P(n) es una propiedad referida a los números naturales tal que P(0) es verdadera y tal que de suponer la verdad de P(n) se puede deducir la verdad de P(n + 1) entonces P(n) es verdadera para todo n natural.

(A la parte 2 – A la parte 4)