Recordemos que Fabián quería demostrar esta afirmación: si a, b, c, d son los vértices de un cuadrilátero cualquiera entonces hay un cuadrado cuyos lados, o sus prolongaciones, pasan por esos cuatros puntos (un lado, o prolongación, por cada punto diferente).
Para probarlo hace la siguiente construcción:
1) Trazamos los segmentos ab y bc. Llamamos a1 y c1 a los puntos medios de ab y bc respectivamente.
2) Trazamos el segmento que une a1 con c1 y agregamos los segmentos que faltan para completar un cuadrado. Llamamos a2 y c2 a los otros dos vértices de ese cuadrado.
3) Trazamos la recta que pasan por a y a2, y la recta que pasa por c y. Llamamos x al punto de intersección de ambas.
4) Trazamos la recta que pasa por d y x. Ésta es una de las rectas que determinan el cuadrado buscado, las otras tres se completan fácilmente.
En realidad, hay dos cuadrados que se pueden trazar a partir del segmento a1 c1, ambos simétricos con respecto a ese segmento. Obtenemos así dos cuadrados que pasan por a, b, c y d.
Si tomamos los segmentos ac y cb obtenemos otros dos cuadrados, los segmentos ca y ab nos dan otros dos. Es decir, usando los puntos a, b, c tenemos ocho cuadrados. Otros ocho salen de a, b, d, y otros ocho de b, c, d. En total hay 24 cuadrados que pasan por a, b, c, d. Fin de la demostración. ¿Qué te parece?
Victoria: Hay varios puntos criticables en tu demostración. Algunos dudosos, otros erróneos. En el punto 3), por ejemplo, deberías demostrar que la recta que pasa por a y a2 en efecto se corta con la que pasa por c y c2.
F: Claro que se cortan, se ve en el dibujo.
V: Pero un dibujo no puede reemplazar a un razonamiento. El dibujo sólo sirve como apoyo, como ayuda para que entendamos el razonamiento en sí (ya que nuestro cerebro ha evolucionado de tal forma que nos resulta más fácil percibir una figura que una idea en abstracto), pero un dibujo en sí mismo puede ser muy engañoso. Por ejemplo, puede haber situaciones especiales en las que el dibujo sea imposible de realizar.
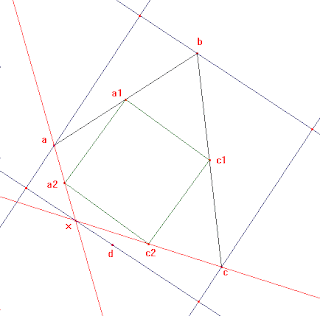
En este caso en particular tu dibujo no nos muestra que hay situaciones en las que las dos rectas en cuestión coinciden. Te muestro un ejemplo (en el dibujo falta el punto d, porque su posición no es relevante a los efectos del ejemplo):

V: Te hago notar que este ejemplo invalida tu demostración, pero no necesariamente el teorema, ya que de todos modos puede ser que exista algún punto x que permita hacer tu construcción.
F: ¿Cómo puede invalidar el razonamiento sin invalidar el teorema?
V: Quiero decir que tal vez lo que afirma el teorema sea cierto, pero que tu razonamiento no lo prueba. Por lo menos, seguro que no lo prueba en el ejemplo que te mostré, ya que en ese caso el razonamiento no puede completarse.
F: De todos modos tu ejemplo no viene al caso.
V: ¿Por qué?
F: Porque estás mostrando un ejemplo de un cuadrilátero “específico”, mientras que yo hablo de un cuadrilátero “cualquiera”.
V: En matemática la palabra “cualquiera” quiere decir “todo”. El teorema debería comenzar así: “Para toda cuaterna de puntos a, b, c, d que sean los vértices de un cuadrilátero...” (Por cierto, que sean los vértices de un cuadrilátero sólo significa que no haya tres alineados.) El uso de la palabra “cualquiera” significa que el razonamiento que se hace se puede aplicar a cualquier situación específica, que se puede repetir en cualquier ejemplo específico que cumpla las condiciones indicadas en las hipótesis. Y no es ése el caso de tu razonamiento.
V: Por otra parte, aun cuando las rectas que pasan por a y a2 y por c y c2 se corten, puede suceder que se corten justo en el punto d (o sea que x = d) por lo que la construcción también sería imposible. (Nuevamente, esto invalida el razonamiento, pero no necesariamente el teorema en sí.)
F: ¿Cómo puede ser que d y x coincidan si d es un dato y x se construye después?
V: La posición de x depende sólo de a, b y c. Supongamos que te doy cuatro puntos a, b, c y d, pero que ubico al punto d en la posición que (en tu construcción) ocupará x. En ese caso no hay modo de completar tu construcción.
F: Insisto ¿cómo puede ser que d y x coincidan si d uno está dado antes y el otro se construye después?
V: “Antes” o “después” no significan nada en este caso. Si ingreso el número 2 en la fórmula x^2 – 2 vuelvo a obtener 2. “Antes” tenía un 2 y “después” tengo el mismo número 2 (y no “otro 2 diferente”). En la situación que te describí d y x coinciden. Es evidente que esto puede suceder porque, insisto, x depende sólo de a, b y c por lo que puedo mover al punto d hasta donde yo quiera sin que x se mueva, por lo que bien puede suceder que d y x coincidan.
Claro que en ese caso podríamos intentar la misma construcción con a, b y d, y así obtener un cuadrado diferente...
F: ...ya te dije que hay 24...
V: ...pero si a, b, c, d son los vértices de un cuadrado entonces ninguno de los 24 puntos que se obtienen con tu construcción sirve para construir un cuadrado como el que el teorema pide. Sin embargo, en ese caso hay infinitos cuadrados posibles (todos los cuales se obtienen de una manera diferente a la que indicaste en tu razonamiento).
F: ¡Pero un cuadrado es un cuadrilátero específico!
V: Ya te respondí a eso: si tu razonamiento fuese correcto debería poder aplicarse a cualquier situación en especial, y en particular si a, b, c, d son los vértices de un cuadrado. Además, el ejemplo de a, b, c, d en los vértices de un cuadrado no sólo refuta tu demostración, sino también tu afirmación de que hay sólo 24 cuadrados que cumplen las condiciones del teorema, ya que, al menos en ese caso, hay infinitos.
F: Entonces ¿el teorema es cierto o no? ¿Mi demostración es correcta o no?
V: Tu demostración no es correcta: no se aplica a todos los casos posibles. Tu dibujo describe una situación que es “falsa” para muchas posiciones de a, b, c y d. En cuanto al teorema, no lo sé. Tal vez sea cierto. Parece que sí lo es en muchos casos, pero no queda claro si vale con toda la generalidad que el enunciado pide.
No discutiremos aquí la validez del teorema, ni tampoco algunos otros puntos dudosos (o al menos poco claros) de la demostración de Fabián, como por ejemplo si, en efecto, el cuadrilátero que aparece pintado de azul en el primer dibujo es realmente un cuadrado. Aquí terminamos el análisis de esta "demostración". Los lectores pueden, si así lo desean, comentar otros puntos de ella. La saga seguirá por nuestra parte, en una próxima entrada, con un tema diferente. Nos vemos.
(A "Falacias y confusiones 2" / A “Falacias y confusiones 1 – Primera parte")
2 comentarios:
En la construccion de Victoria,la recta que pasa por a y a2 y la que pasa por c y c2 son coincidentes entre si, puesto que todos esos puntos resultan alineados. Sin embargo, la interseccion buscada, que es el punto x, existe y se encuentra en la proyeccion de b sobre las rectas mencionadas.
Trazando una recta que pase por el punto d (no dibujado) y por x, esa recta es uno de los lados del cuadrado que buscamos, precisamente el lado que pasa por el punto d. Es muy sencillo ahora encontrar las rectas que pasan por
a, b y c.
Construido el cuadrado buscado, es muy facil demostrar que es un cuadrado.
Ecs.
Así como Bernoulli dejó planteado el problema de la braquistócrona después de haberlo resuelto, dejo planteado mis teoremas dejando la comprobación para los que puedan llegar a leer este comentario.
No incluyo las demostraciones principalmente porque son trabajosas y no tengo tiempo de volcarlas a un soporte informático para que sean leídas con claridad (y además porque algunos puntos no los demostré de manera formal, sólo de manera sugestiva).
Teorema nº1: Dados cuatro puntos en el plano, es posible trazar infinitos rectángulos cuyos lados, o sus prolongaciones, incluyan, cada uno, uno y solo uno de los mencionados puntos.
Teorema nº2: Dados cuatro puntos cualesquiera en el plano, siempre pueden trazarse doce cuadrados distintos que los incluyan en sus lados (o sus prolongaciones) de la misma manera que para los rectángulos del Teorema 1.
Teorema nº3: En el caso especial de que los cuatro puntos antedichos se hallen formando un cuadrado, los cuadrados que puedan trazarse de la manera descrita en los dos teoremas anteriores serán infinitos y siempre contendrán los cuatro puntos dentro de sus lados si el área del cuadrado obtenido es mayor a la del cuadrado original (en donde los puntos son sus vértices). Si el área del cuadrado obtenido resulta menor, los cuatro puntos dados estarán todos en las prolongaciones de sus lados.
Corolario nº1: Si los puntos se hallan todos sobre la misma recta, las áreas de los 12 cuadrados obtenidos se repetirá entre dos y seis veces.
Corolario nº2: Si dos puntos cualesquiera P1 y P2 están incluidos dentro de una recta ortogonal a otra que contenga a los puntos P3 y P4, podrán trazarse los cuadrados mediante métodos distintos a los obtenidos en cualquier otro caso. Para el caso de una recta que pase por P1 paralela a la que pasa por P2, se obtendrá una pareja de cuadrados cuyos lados son paralelos entre sí, cuyos vectores de dirección guardan con los vectores de dirección de las rectas ortogonales antedichas una relación sencilla.
Nota nº1: Obsérvese que la aclaración del "Teorema de Pasin" de que los cuatro puntos deben formar un cuadrilátero cualquiera es innecesaria. De hecho pueden formar un triángulo o una linea recta sin invalidar el razonamiento de existencia de al menos un cuadrado que cumpla las exigencias.
Nota nº2: No me molesté en deducir si la construcción de Fabián es correcta. Intuyo que sí, pero que no es válida para obtener todos los cuadrados posibles, tal como aclaró Victoria.
Nota nº3: No hay 24 cuadrados posibles, al menos no en lo que pude deducir utilizando Geometría Analítica, sino 12. Si se utiliza la "relación sencilla" (que deberá ser deducida) mencionada en el Corolario 2 cuando no se dan las condiciones de ortogonalidad, se obtiene un rectángulo y no un cuadrado. Claro que es un rectángulo algo especial y no totalmente trivial, que deberá deducir el matemático avezado.
Bien, en todo caso las cartas están sobre la mesa. Me tomó unas 8 horas llegar a estos interesantes resultados, espero que puedan demostrarlos ustedes mismos. Cuando tenga tiempo, dentro de algunos meses, quizá publique las demostraciones si nadie lo hace antes.
Publicar un comentario