(Ésta es la transcripción de mi charla en el 4º Encuentro para Celebrar el Ingenio de Martin Gardner y Jaime Poniachik.)
El universo en el que transcurre este pequeño Big Bang es una cinta dividida en casillas todas iguales; es necesario aclarar que la cinta es infinita, en el sentido de que puede ser prolongada indefinidamente por cualquiera de sus dos extremos:
Este universo contiene solamente tres tipos de partículas, a las que llamaremos A, B y C. Una "ley natural" dice que cada casilla puede contener como máximo una partícula.
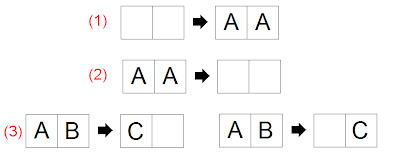
Hay tres reglas que rigen el modo en el que las partículas son creadas o destruidas. Estas reglas están resumidas en la siguiente imagen:
Regla 1: En dos casillas vacías consecutivas pueden colocarse dos letras iguales (en la imagen se ejemplifica con AA, pero también puede ser BB o CC).
Regla 2: Es la inversa de la anterior; dos letras iguales consecutivas pueden ser borradas (como antes, en la imagen se ejemplifica con AA, pero también puede ser BB o CC):
Reglas 3: Dos letras diferentes consecutivas pueden ser reemplazadas por la tercera letra, es decir, las dos letras se borran y el lugar que ocupaba una de ellas pasa a ser ocupado por la otra letra. En la imagen se ejemplifica el reemplazo de AB por C, pero también vale para reemplazar BA por C, CA por B, AC por B, etc.
Veamos un ejemplo de aplicación de las reglas:
En el ejemplo hemos partido del universo vacío y hemos llegado a la configuración A-espacio-B-espacio-C. Esto se ha conseguido en seis pasos; un "paso" consiste siempre en la aplicación de una de las tres reglas.
En los desafíos se parte de una cierta configuración y se debe llegar a otra, siempre en la menor cantidad posible de pasos. Los desafíos están resumidos en esta imagen:
Desafío (a): Partir del espacio vacío y llegar a ABC (sin espacios intermedios). Se entiende que al terminar la cinta sólo muestra ABC, el resto del universo está vacío. Yo lo logré en 10 pasos, pero la solución no es necesariamente la óptima. De hecho, la noche misma del encuentro Pablo Coll me aseguró que había encontrado una solución en solamente 6 pasos y que después me la enviaría.
Desafío (b): Partir de ABC y llegar a BCA; las tres letras finales no tienen por qué ocupar las mismas casillas que las iniciales. Yo lo logré en 10 pasos, pero la solución no es necesariamente la óptima.
Desafío (c): Partir de ABC y lograr que se vayan formando sucesivamente las otras cinco permutaciones posibles de esas tres letras (ACB, BCA, BAC, CAB y CBA, no necesariamente en ese orden). En su momento, cada permutación debe aparecer sola en la cinta; la cuenta de los pasos termina en el momento en que aparece la sexta permutación (sea cual fuere).
En los dos últimos desafíos, para hacerlos más interesantes, no doy cantidades de pasos:
Desafío (d): Partir de la cinta vacía y llegar a A.
Desafío (e): Partir de A y llegar a B (la B no debe ocupar necesariamente la misma casilla que la A).
Las soluciones que lleguen (por mail o dejadas en los comentarios) serán publicadas aquí mismo, más abajo.
Gracias... ¡y que se diviertan!
Soluciones:
(a) Pablo Rowies dio en los comentarios una solución para el desafío (a) en 8 pasos que Claudio Meller, también en los comentarios, mejora a 6 pasos y Marcos Donnantuoni, a 5:
0 - - - -
1 - - AA
2 AAAA
3 A - - A
4 ABBA
5 ABC
(b) Pablo Rowies da una solución en 8 pasos para el desafío 2 que Claudio Meller mejora a 6 pasos y Marcos Donnantuoni, a 5:
0 ABC -
1 AA - -
2 AAAA
3 A - - A
4 ABBA
5 - CBA
(c) Marcos Donnantuoni y Claudio Meller encuentran soluciones con 25 pasos, tras un estudio informático Marcos aclara que la solución es óptima.
0__________ABC__
1__________ABCBB
2__________ABA_B
3__________AC__B
4__________ACBBB
5__________ACB__ *
6___________BB__
7_________BBBB__
8_________B__B__
9_________BAAB__
10________BAC___ *
11________BB____
12________BBBB__
13________B__B__
14________BCCB__
15________BCA___ *
16______CCBCA___
17______CCB_B___
18______CA__B___
19______CABBB___
20______CAB_____ *
21______CC______
22____CCCC______
23____C__C______
24____CBBC______
25____CBA_______ *
Soluciones óptimas:
Desafío (a): 5 pasos (Marcos Donnantuoni), no puede mejorarse.
Desafío (b): 5 pasos (Marcos Donnantuoni), no puede mejorarse.
Desafío (c): 25 pasos (Claudio Meller y Marcos Donnantuoni), no puede mejorarse.
Gracias por los comentarios en los que se plantean otros desafíos, en breve los incorporaré a una nueva entrada sobre el tema. Por supuesto, también agradezco los comentarios con soluciones, las que corresponde a los nuevos desafíos también aparecerán próximamente en otra entrada sobre este tema.
Éste es el video de la charla.



14 comentarios:
Si entendí bien el juego...
Desafío 1:
|B|B|_|_|_|_| (1)
|B|B|A|A|_|_| (2)
|B|B|A|A|C|C| (3)
|B|C|_|A|C|C| (4)
|B|C|_|_|B|C| (5)
|B|C|A|A|B|C| (6)
|B|B|_|A|B|C| (7)
|_|_|_|A|B|C| (8)
Si, se puede hacer en seis pasos:
AA
AACC
A.BC
A..A
ABBA
ABC
Desafío 2:
|_|_|A|B|C|_|
|_|_|A|A|_|_| (1)
|B|B|A|A|_|_| (2)
|B|C|_|A|_|_| (3)
|B|C|_|A|C|C| (4)
|B|C|_|_|B|C| (5)
|B|C|A|A|B|C| (6)
|B|C|A|_|C|C| (7)
|B|C|A|_|_|_| (8)
Si, se puede hacer en seis pasos:
AA
AACC
A.BC
A..A
ABBA
ABC
Para pasar de ABC a CBA
ABC
CC
CCBB
C.AB
C..C
CBBC
CBA
Tengo una demostración de que los desafíos D y E son bastante más difíciles de lograr... :)
Una solución en cinco pasos para el desafio 1:
0 ....
1 ..AA
2 AAAA
3 A..A
4 ABBA
5 ABC.
Una en 5 pasos para el desafío 2:
0 ABC.
1 AA..
2 AAAA
3 A..A
4 ABBA
5 .CBA
Un lado interesante del problema es pedir soluciones que usen poco «espacio» además o en lugar de usar pocas operaciones.
También se podría hacer "caminar" a una A, es decir, partiendo de A, en cuántos pasos se la puede mover n casilleros hacia la derecha o izquierda...
Gracias por las sugerencias de nuevos desafíos. Las recogeré próximamente en una nueva entrada sobre el tema. Saludos,
Mientras tanto, un desafío "escatológico": a ver quién convierte BABA en CACA en la menor cantidad de pasos :)
Encontré una solución en 25 pasos para el desafío (C) que sólo utiliza 5 "espacios":
00 ABC--
01 C-C--
02 C-CAA
03 C--BA
04 CCCBA
05 --CBA
06 --C-C
07 BBC-C
08 BA--C
09 BACCC
10 BAC--
11 B-B--
12 B-BAA
13 B--CA
14 BBBCA
15 --BCA
16 --B-B
17 AAB-B
18 AC--B
19 ACBBB
20 ACB--
21 -BB--
22 -BBBB
23 -B--B
24 -BAAB
25 --CAB
Por otra parte, se puede hacer "caminar" una A una cantidad par N de casilleros a la izquierda (o a la derecha), en exactamente N pasos; por ejemplo para N=4
00 A----
01 AAA--
02 --A--
03 --AAA
04 ----A
Para moverla sólo un lugar, cuesta un poquito más de trabajo, a mí me salió en 5 pasos (y utilizando dos "espacios" adicionales en sentido opuesto al que queremos "avanzar"):
00 --A-
01 BBA-
02 BC--
03 BCAA
04 BB-A
05 ---A
Tengo una solución para mover A un paso a la derecha en 3 pasos:
00 -A--
01 -ABB
02 --CB
03 --A-
Publicar un comentario