1. Tres conjeturas
Rodolfo Kurchan me ha hecho llegar por línea privada la siguiente conjetura:
Conjetura de Kurchan: Fijado un par de números n y m, en todas las caminatas marcianas que recorran completamente el rectángulo de n x m la suma de los números obtenidos será la misma. (No se obtendrán necesariamente los mismos números, pero sí será la misma la suma de todos ellos).
Por ejemplo, todas las caminatas marcianas que recorren el cuadrado de 3 x 3 suman 20.
Podemos extender la conjetura de la siguiente manera:
Conjetura ampliada: Fijada una región R del cuadriculado que pueda ser recorrida completamente por una caminata marciana, en todas las caminatas marcianas que recorran completamente R la suma de los números obtenidos será la misma.
La conjetura ampliada puede extenderse más todavía. Tomemos, por ejemplo, un grafo que admita un camino hamiltoniano (es decir, un camino que visite todos los nodos del grafo exactamente una vez cada uno, entendiendo que no vuelve al nodo inicial). A cada nodo del grafo le asignamos un número siguiendo el orden en que fue visitado y según la regla de la caminata marciana: cuando el camino pasa por un nodo, éste recibe el número que indica la cantidad de números que están conectados con él en ese momento. Un ejemplo:
Hay una demostración bastante simple (una vez que a uno se le ocurre) de la conjetura para grafos. Esta conjetura, como es evidente, tiene a las otras dos como casos particulares. Dejo, para quienes les interesen esas cosas, el desafío de encontrar la demostración. Una pista: la suma que se obtiene es la cantidad de lados del grafo. De este modo las tres conjeturas pasan a ser "teoremas", pero seguiré llamándolas "conjeturas" de todos modos.
2. El Triángulo de Kurchan
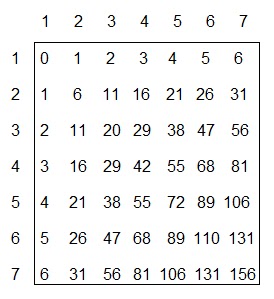
La conjetura de Kurchan nos habilita para construir el siguiente cuadro:
En la posición (n,m) del cuadro ponemos la suma de una caminata marciana que recorra completamente el rectángulo de n x m. (Por supuesto, el cuadro sigue infinitamente hacia la derecha y hacia abajo, aquí sólo hemos mostrado un fragmento.) Rodolfo prefiere girar el cuadro 45° y disponer los números en un triángulo al que (en analogía con el Triángulo de Pascal) llamaremos el Triángulo de Kurchan:
Rodolfo ha investigando el triángulo y encontró en él algunas propiedades curiosas. He aquí una lista:
1. La primera diagonal se obtiene sumando 1 cada vez, la segunda se obtiene sumando 5, la siguiente sumando 9, la siguiente sumando 13, etc.
2. En la segunda columna del triángulo aparece la sucesión 1, 11, 29, 55, 89,... que es http://oeis.org/search?q=1%2C11%2C29%2C55%2C89&sort=&language=english
3. La suma de los cuatro vecinos a cada "agujero" de la columna central (por ejemplo: 0 + 1 + 1 + 6 = 8; 6 + 11 + 11 + 20 = 48;...) forman la sucesión 8, 48, 120, 224,... que corresponde a los óctuples de los números hexagonales. Véase también: http://oeis.org/search?q=8%2C48%2C120%2C224%2C360%2C528&sort=&language=english
4. La diagonal a "salto de caballo" 0, 11, 38, 81,... es http://oeis.org/search?q=0%2C11%2C38%2C81&sort=&language=english
5. La suma de lo números en cada fila da 0, 2, 10, 28, 60, 110, 182,... que es el doble de la suma de los n primeros cuadrados consecutivos. Véase: http://oeis.org/search?q=2%2C10%2C28%2C60%2C110%2C182%2C280&sort=&language
6. Elijamos un número cualquiera del triángulo, pero que no esté en el borde. Tomemos sus dos vecinos de la izquierda y de la derecha, el número que está justo arriba del elegido y el que está justo abajo. La suma de esos cuatro números será el cuádruple del número elegido. Por ejemplo, si elegimos el 11 tenemos que 3 + 11 + 1 + 29 = 44 = 4 x 11.
7. Si sumamos cada número de la columna central con su vecino de abajo a la izquierda obtenemos: 0 + 1 = 1; 6 + 11 = 17; 20 + 29 = 49;... que es la sucesión de los números hexadecagonales centrados. Véase: http://oeis.org/search?q=1%2C17%2C49%2C97&sort=&language=english
Por supuesto, están todos invitados a encontrar otras propiedades u otros datos curiosos del Triángulo de Kurchan.
5 comentarios:
La suma de las caminatas de los cuadrados nxn (1x1, 2x2, 3x3) etc da 0,6,20,42,72 siendo la fórmula 4n^2-6n+2 los valores coinciden con https://oeis.org/A002943, pero la fórmula es distinta porque la serie empieza en n=cero (offset) y las caminatas con n=1
Muy buena conjetura!
Se me ocurre esta demostración (la pongo en rot13 para no arruinar, la pueden descodificar copiando el texto en rot13.com):
Cbqrzbf ire ry cebprfb qry erpbeevqb pbzb fvthr: ny pbzvramb, gbqbf ybf abqbf rfgáa fva znepne, l ybf ynqbf gvrara ha 0.
N zrqvqn dhr hab in znepnaqb abqbf pba aúzrebf, in cbavraqb ra ybf ynqbf dhr yb gbpna ha 1 (fv ln gvrara ha 1, fr yb qrwn pbzb rfgá). Ry aúzreb pba dhr fr znepn pnqn abqb rf yn fhzn qr ybf inyberf qr fhf ynqbf.
Pbzb ry erpbeevqb gbpn gbqbf ybf abqbf, sbembfnzragr gbqbf ybf ynqbf freáa znepnqbf pba 1; l rfgbf 1f ahapn fr phragna záf qr han irm cnen pbzchgne ry pbagravqb qr ybf abqbf; qr znaren dhr ny svany gbqbf ybf abqbf fhzneáa gnagb pbzb ybf ynqbf qry tensb.
¿Es válido mi razonamiento?
Me parece que el razonamiento es perfectamente correcto.
Hola Gustavo:
Un tema apasionante. Lamento no tener tiempo para ponerme con la debida dedicación.
No obstante, creo que encontré la función que, dados n y m, nos da la suma de la caminata marciana que recorre completamente un rectángulo de n x m. LLamemos K(n,m) a dicho número (en honor a Kurchan). Entonces
k(n,m)=4nm-3(n+m)+2
En realidad, no encontré la función para todo n y m; esto es solo una conjetura más. La deduje simplemente estudiando las relaciones entre los numeros de tu tabla.
Saludos.
Cristian me ha pedido que publique este comentario en su nombre (que reemplaza uno anterior, suprimido a pedido suyo):
La función que conjeturé hace un rato, puede probarse para todo n y m. La repito:
K(n,m) = 4nm – 3(n+m) + 2
Donde K(n,m) es la suma de la caminata marciana que recorre un rectángulo de n x m.
Lo probamos por inducción sobre m.
Para m=1, verificamos rápidamente que K(n,1) = n-1 (hacer las cuentas); lo que resulta ser cierto porque en un rectangulo de n x 1, las caminatas son de la forma 0,1,1,1,1,… donde el 1 se repite n-1 veces.
Supongamos que la hipótesis se verifica para K(n,m) y veamos que se verifica para K(n,m+1)
Digamos que n es la cantidad de filas horizontales y m la cantidad de columnas verticales.
Como todos los recorridos suman lo mismo, podemos elegir el que nos convenga para la prueba. Observemos entonces que siempre podremos recorrer el rectángulo de modo de terminar el recorrido en el casillero superior derecho. Así, agregar una columna siempre consistirá en desplazarnos desde allí a la casilla de la derecha y luego descender hasta cubrir todas las filas del rectángulo, completando entonces un rectángulo de n x m+1 (¡Hacer los dibujitos! Yo no se como hacerlos aquí).
Entonces a K(n,m), solo debemos sumarle la suma de los números de la columna agregada y verificar si esto resulta ser igual a K(n,m+1).
Si el rectángulo tiene una sola fila, y entonces es de 1 x m, agregar una columna representa desplazarnos un casillero a la derecha y anotar 1, esto es, solo sumamos 1 a K(1,m) y eso es lo que suma la caminata de 1 x m+1
Si el rectángulo tiene dos filas, y entonces es de 2 x m, agregar una columna a la derecha representa agregar de arriba hacia abajo: 2;3, cuya suma es 5, de modo que a K(2,m) debemos sumarle 5, y eso es lo que suma la caminata de 2 x m+1
Si el rectángulo tiene tres o más filas, y entonces es de n x m (con n>2), agregar una columna a la derecha representa agregar de arriba hacia abajo: 2;4;4;4;…;4;3, donde el 4 se repite n - 2 veces (verificarlo), esto es, se suma 5 + 4(n-2) a K(n,m).
Ahora podemos ver que en los dos casos anteriores, con una y dos filas (n=1 y n=2) también sumábamos 5 + 4(n-2) a K(n,m) pues 5 + 4(1-2) = 1 y 5 + 4(2-2) = 5; y en efecto sumábamos 1 y 5 respectivamente.
Así pues, para todo n, supuesto el caso para K(n,m), la suma de los números de un rectángulo de n x m+1 es igual K(n,m) + 5 + 4(n-2).
La prueba inductiva se completa si verificamos que esto último es justamente K(n,m+1), esto es, basta verificar que
K(n,m+1) = K(n,m) + 5 + 4(n-2)
lo que se comprueba algebraicamente reemplazando K por su definición, resolviendo a la izquierda, resolviendo a la derecha y verificando que en ambos casos da lo mismo.
Saludos
Publicar un comentario